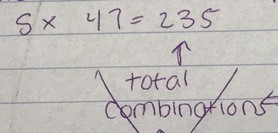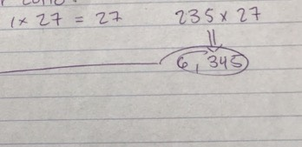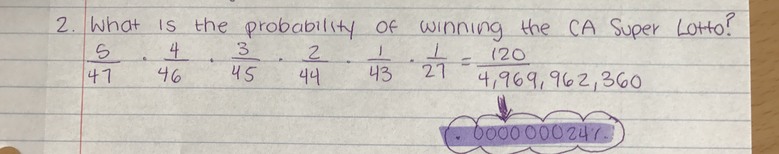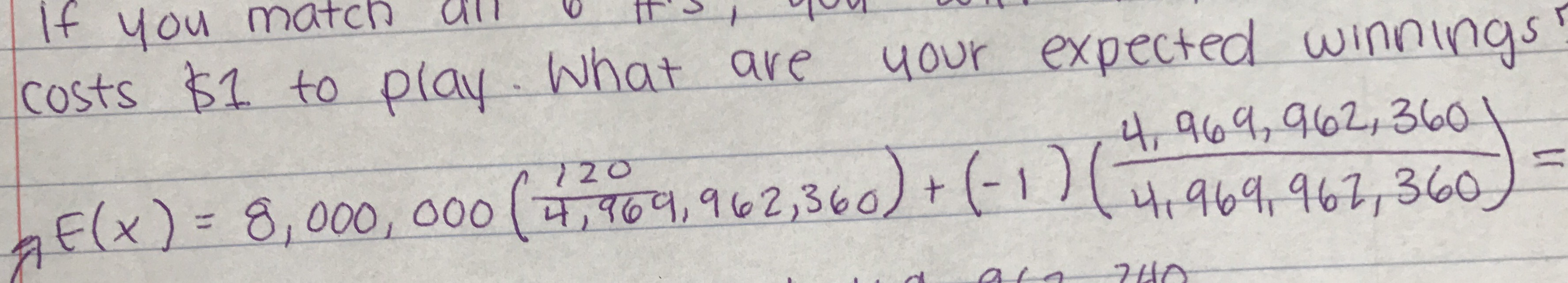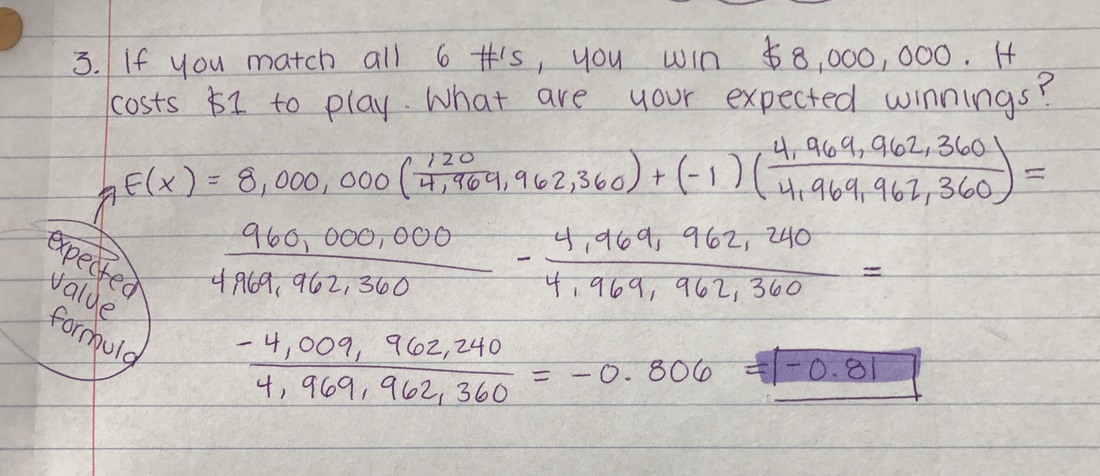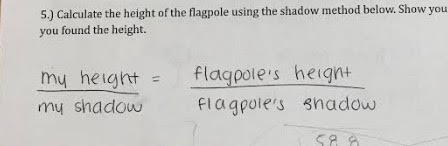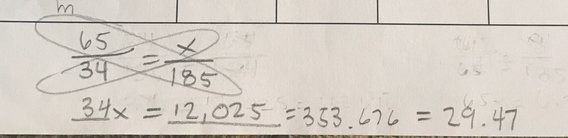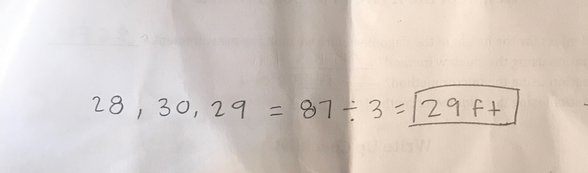Fireworks Problem
Problem statement:
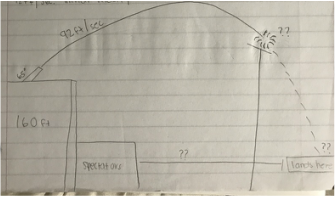
A school wants to have a firework display in order to celebrate that their soccer team won the championship. The director doesn't really care about the cost of the show, but he does care about the safety of the spectators. We know that fireworks will be launched from a 65 degree angle, the initial velocity is 92 ft./sec., and the height of the towers is 160 ft. We have fo find the vertex and the distance that the fireworks will travel in order to know that they spectators will be safe.
Process:
The first day we started this problem, we had to draw a sketch of the tower in order to be able to vizualize it better. This is how my drawing first looked:
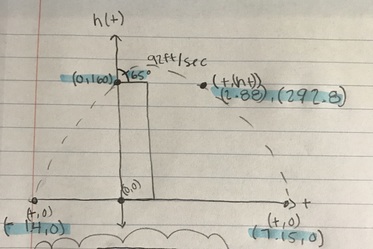
The next day, after looking back at our drawings, we decided to create an xy table. It would help us find out what at what time the fireworks would reach its vertex. Before doing the xy table, we knew we needed to have an equation in order to fill it out. The equation we used was: h(t) = 160 + 92t - 16t^2. This is how my xy table and my equations looked:

While working on the xy table, we found out that the maximum height was at 3 seconds. Then we solved for the height at 2.5 seconds, and it was higher than 3 seconds, with this we realized that the max height was going to be betweem 3-2 seconds.
Since there are many numbers between 3-2, we knew we couldn't just keep plugging in numbers inside our equation, it was time to move on and find another way to find the vertex.
Since there are many numbers between 3-2, we knew we couldn't just keep plugging in numbers inside our equation, it was time to move on and find another way to find the vertex.
For the next couple of weeks, we worked on multiplying binomials, from there we worked on factored intercepts, and then we put those things together in order to find points in a parabola (x intercepts, y intercept, vertex). After all of this, we finally got to the point where we worked on the quadratic formula.
This is how the quadratic formula looked after plugging in our givens:
This is how the quadratic formula looked after plugging in our givens:

Step by step:
1. Plug in the a, b, c in the quadratic formula
a= 160
b= 92
c= -16
2. Multiply 92^2, you'll get 8,464
3. Multiply 4 by 160, then multiply your answer by -16, you'll get 10,240
4. Multiply 2 by -16, you'll get -32
5. Add 8,464 and 10,240, then find the square root of the answer which is 136.8
6. Adding: 92 + 136.8 = 44.8
Subtracting: -92 - 136.8 = -228.7
7. Divide 44.8 by -32 = -1.4
Divide -228.7 by -32 = 7.15
8. x intercepts: (-1.4,0)(7.15,0)
9. To find the time of the vertex, add both x intercepts, divide them by 2, then subtract the answer (4.27) by 7.15, you'll get 2.88, which is the time of vertex.
1. Plug in the a, b, c in the quadratic formula
a= 160
b= 92
c= -16
2. Multiply 92^2, you'll get 8,464
3. Multiply 4 by 160, then multiply your answer by -16, you'll get 10,240
4. Multiply 2 by -16, you'll get -32
5. Add 8,464 and 10,240, then find the square root of the answer which is 136.8
6. Adding: 92 + 136.8 = 44.8
Subtracting: -92 - 136.8 = -228.7
7. Divide 44.8 by -32 = -1.4
Divide -228.7 by -32 = 7.15
8. x intercepts: (-1.4,0)(7.15,0)
9. To find the time of the vertex, add both x intercepts, divide them by 2, then subtract the answer (4.27) by 7.15, you'll get 2.88, which is the time of vertex.
To find the height of the vertex, you have to use the equation we first used: h(t) = 160t + 92t - 16t^2 and plug in 2.88.
This is my work:
This is my work:
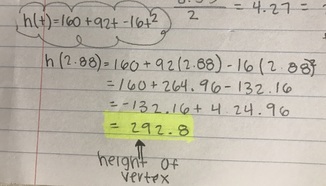
Step by step:
1. Plug in 2.88 for t
2. Multiply 92 by 2.88
3. Multiply -16 by 2.88^2
4. Add 160 by 264.96
5. Add -132.16 by 424.96
6. Get height of vertex: 292.8
1. Plug in 2.88 for t
2. Multiply 92 by 2.88
3. Multiply -16 by 2.88^2
4. Add 160 by 264.96
5. Add -132.16 by 424.96
6. Get height of vertex: 292.8
To find the distance you have to use this equation: d(t) = 92t/ tan65.
This is my work:
This is my work:

Step by step:
1. Plug in 7.15 for t
2. Multiply 92 by 7.15, you'll get 657.8
3. Divide 657.8 by tan65
1. Plug in 7.15 for t
2. Multiply 92 by 7.15, you'll get 657.8
3. Divide 657.8 by tan65
This is how my drawing of the tower looks now:
Problem Evaluation:
In all honesty, I didn't like working on this problem. I feel like the process was really long (about 12 weeks) and the answer was really simple. Maybe if we had solved this in another way, or approached it in a different way I would've enjoyed working on it. I didn't like how we approached it, but I did like how it was challenging for me.
Self Evaluation:
I don't think I deserve a really high grade on my effort because I didn't really try that much to understand the work. I admit that there were times that I did try to understand what was going on, for example, when we solved for the vertex, or when we solved for the quadratic formula, but not most of the time. I think I might deserve either a B- or a C.
California Super Lotto Problem
Problem Statement:
In class, we started playing the CA Super Lotto, while doing so, we learned that there are 3 rules. The rules are:
1. Choose any 5 #'s between 1-47 (these will not repeat)
2. Pick a mega # between 1-27 (this # may repeat)
3. Match all 5 #'s and the mega # and you win!
After playing, no one won. We continued class learning more about probability. In this problem, we had to find how many possible number combinations are possible, what is the probability of winning the CA Super Lotto, and what is our expected winnings if we match all 6 numbers.
1. Choose any 5 #'s between 1-47 (these will not repeat)
2. Pick a mega # between 1-27 (this # may repeat)
3. Match all 5 #'s and the mega # and you win!
After playing, no one won. We continued class learning more about probability. In this problem, we had to find how many possible number combinations are possible, what is the probability of winning the CA Super Lotto, and what is our expected winnings if we match all 6 numbers.
Process & Solution:
#1. How many different number combinations are possible for a CA Super Lotto ticket?
My initial guess for the total combinations was only 235. I got this by multiplying 5 x 47. I multiplied this because there are 5 numbers you have to pick and times 47 because you have to pick a number between 1-47. After taking a second look at my answer I realized that 235 was a really small number to be the right answer, so I took another step. I multiplied 235 by 27. I multiplied by 27 because I realized that I needed to include the mega number too, I got 6,345. I really thought I had gotten it right, but the answer seemed really small too.
My initial guess for the total combinations was only 235. I got this by multiplying 5 x 47. I multiplied this because there are 5 numbers you have to pick and times 47 because you have to pick a number between 1-47. After taking a second look at my answer I realized that 235 was a really small number to be the right answer, so I took another step. I multiplied 235 by 27. I multiplied by 27 because I realized that I needed to include the mega number too, I got 6,345. I really thought I had gotten it right, but the answer seemed really small too.
Then I saw some of my classmates approaching the problem in a different way. They were multiplying 5 by 47 then the product by 46, then the same with 45,44, and 43. Five was being multiplied by these numbers because that's the sample space, the numbers kept getting smaller because you cannot repeat a number. After multiplying, the answer was 184, 072, 360. I thought I had finally found the answer until I realized I had forgotten the mega number. I multiplied 184, 072, 360 by 27 because that's the sample space of the mega number. The answer was 4, 969, 962, 360. Now, the answer did make sense because it was really big.
#2. What is the probability of winning the CA Super Lotto?
To find the probability of winning, we had to multiply this: 5/47 x 4/46 x 3/45 2/44 x 1/43 x 1/27 . You multiply those numerators because that's the amount of numbers you have to pick and the denominators because it starts with the sample space. The last fraction you have to multiply by 27 because that's the sample space for the mega number. After multiplying, you get 120/4, 969, 962, 360. After getting another fraction, you need to find the percentage: .000000024%. That is the probability of winning the CA Super Lotto.
To find the probability of winning, we had to multiply this: 5/47 x 4/46 x 3/45 2/44 x 1/43 x 1/27 . You multiply those numerators because that's the amount of numbers you have to pick and the denominators because it starts with the sample space. The last fraction you have to multiply by 27 because that's the sample space for the mega number. After multiplying, you get 120/4, 969, 962, 360. After getting another fraction, you need to find the percentage: .000000024%. That is the probability of winning the CA Super Lotto.
#3. If you match all 6 numbers, you win $8,000,000. It costs $1 to play. What are your expected winnings?
To find the answer, I had to use the formula we learned last week in class. It was, what I like to call, the expected value formula, I'm not really sure what the real name of it is. This is it: E(X)=∑xipi
For x, I pluggled in 8,000,000 because that's how much you would win if you matched all 6 #'s. Then you plug in for i the probability of winning which is (120/4,969, 962, 360)and multiply it. Then you have to add -1 and multiply that by your other i which is,
(4,969, 962, 360/4,969, 962, 360). This is how my work looked so far:
To find the answer, I had to use the formula we learned last week in class. It was, what I like to call, the expected value formula, I'm not really sure what the real name of it is. This is it: E(X)=∑xipi
For x, I pluggled in 8,000,000 because that's how much you would win if you matched all 6 #'s. Then you plug in for i the probability of winning which is (120/4,969, 962, 360)and multiply it. Then you have to add -1 and multiply that by your other i which is,
(4,969, 962, 360/4,969, 962, 360). This is how my work looked so far:
The next step is to multiply 8,000,000 by 120 and you'll get 960,000,000. You then plug in that number in the fraction and it'll be (960,000,000/4, 969, 962, 360). Then you'll multiply the -1 by 4, 969, 962, 360 and you'll get (-4, 969, 962, 340/ 4, 969, 962, 360). Finally, when u subtract those big fractions you'll get (-4,009, 962, 240/4, 969, 962, 360). The answer/ expected winnings is -0.81
This is my work:
This is my work:
Problem Evaluation :
I actually really liked this problem because I could really understand it, even though I was a bit confused in the beginning. I really liked how we were able to use everything we learned in about one month in this one, big problem. It really pushed my thinking because I realized that I wasn't solving it with the skills we had learned from other problems. After solving problem #1, I found connections from other problems I had worked on, so it was easier to solve the 2nd and 3rd problem. What I got out from this problem is that I started talking and helping my partner so I got to understand more about what steps I needed to take in order to solve each problem. Basically, sharing my ideas and working with my classmates helps me understand problems easier.
Self Evaluation:
If I was to give myself a grade on this probability unit, I would give myself a B+. I would give myself this grade based on how much effort and understanding I put into this unit. Since I put more effort (working with classmates and having a positive attitude) in this unit I was able to gain a deeper and stronger understanding about the problems.
Edits: Changed my wording in some paragraphs, fixed some images, write in bold questions.
Height of the HTHCV Flagpole Problem
Problem Statement:
High Tech High wants to get a new flag. In order to do so, they need to figure out the height of the flagpole.
Process & Solution:
My initial guess for the flagpole was between 20 and 25 feet. I thought it needed to be between these numbers because the flagpole had to be at least 5 times my height. The next step, after coming up with a guess, we had to use math to find the real answer. In class, we learned three different methods that would help us find the height of the flagpole, using similarity between two triangles. Similarity is when two polygons have the same shape, but different size. The corresponding sides of the shape have to be proportional and the angles have to be equal.
Shadow Method:
The first method that we used was the shadow method. In this method, we had to measure our height, our shadow's height, and the flagpole's shadow, in order to find the height of the flagpole. Before starting to set up the proportions, we had to prove that the triangles were similar using the AA theorem. We knew both of these triangles were similar because there were two equal angles. One of the angles was a right angle and the second one was from the end of my shadow and the flagpole's shadow. After proving that they are similar, we were able to set up a proportion. It looked like this:
After setting it up, we had to plug in numbers. I plugged in 4'9 for my height, 6'9 for my shadow. I left an x for the height of the flagpole, and 40 ft for its shadow. Then, I converted these numbers into inches. After this, I cross multiplied. My work looks like this:
My answer was 340 inches. I converted it to ft by dividing by 12. My final answer was 28.4 ft using the shadow method.
Mirror Method:
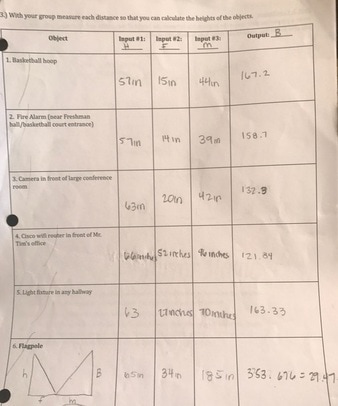
The second method we used was the mirror method. In this method, we had to put a mirror on the floor, then walk backwards until we were able to see the top of the flagpole. We needed to measure our height, the horizontal distance from where we were standing to the mirror, then from the mirror to the flagpole. We then labeled each input and the output. Then we drew a diagram. It looked like this:
After having our diagram and our inputs, we needed to prove that the triangles we looked at were similar. Again, we proved this by using the AA theorem. We knew the triangles were similar because both of them had a right angle and ended (touched) in the same spot. To get some practice, we had to find the height of 6 different objects using this method. We found the height of the basketball hoop, a fire alarm, a camera, a wifi router, a light fixture, and finally the flagpole. Again, we found the heights of each object by setting our height, the horizontal distance from me to the mirror, horizontal distance from the mirror to the object, then x for the object's height, in a proportion. The proportion was: h/f = b/m
To find the height of the flagpole, we plugged in our data, then cross multiplied. Our proportion was: 65in/34in = x/185in. The answer in inches was 353.676. We needed to convert it to feet, so we divided by 12 and got 29.47 feet which rounds up to 30 ft.
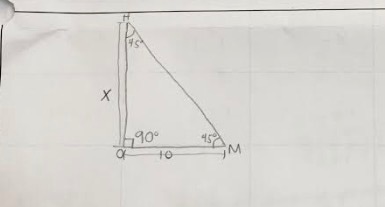
Clinometer Method:
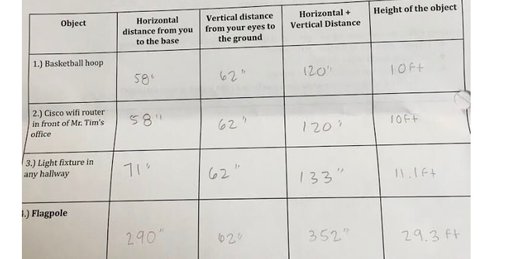
The third method that we used was the clinometer method. In this method, we used an isoceles tringle to find the height of the flagpole. An isoceles triangle is a triangle with a 90 degree angle, and two 45 degree angles. Using this method, we had to use a clinometer provided by Mr. Carter, we had to make sure that the angle that we were using to look at our object was 45 degrees. For this problem, we had to find the heights of different objects too.
For this method, we didn't need to set up a proportion. We just needed to add our horizontal distance from me to the base, and the vertical distance from my eyes to the ground. The horizontal distance was 290 inches and the vertical distance was 62 inches. To find the height of the flagpole, we had to add both of these distances, we go 352 inches. Again, we needed to convert to feet, so we divided by 12 and got 29.30 feet.
My Final Estimation:
For the final height of the flagpole, I added all three final answers, then divided by three to find the average. I decided to do this because the answer had to be in between some of the ones I got. The answer was 29 feet.
Problem Evaluation:
I really liked working in this problem because we used many methods to find the height of the flagpole. I really liked how there wasn't just one way to solve for the problem, there were three ways. What really pushed my thinking is how we found the height of the flagpole using angles and triangles. I really wish I could've but all of my understanding in my test. I did try my hardest, but I just didn't explain why we could use AA theorem, but now I can.
Self Evaluation:
If I were to grade myself in this similarity unit, I would give an A. I would give myself an A because I tried really hard to understand every method. For example, in order to understand the subject, I worked really hard to finish every worksheet we got. I would also work more with my table. My biggest take away from this problem was how not only I learned that there are many ways to find the height, but that the ways to find it are with angles. Since we couldn't measure it with a measuring tape, we found other ways to do so.
Edits: Added more to my self evaluation. Added more to my problem evaluation. Added images and fixed some spelling.