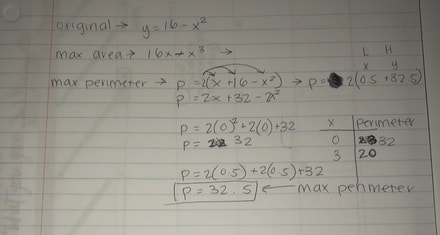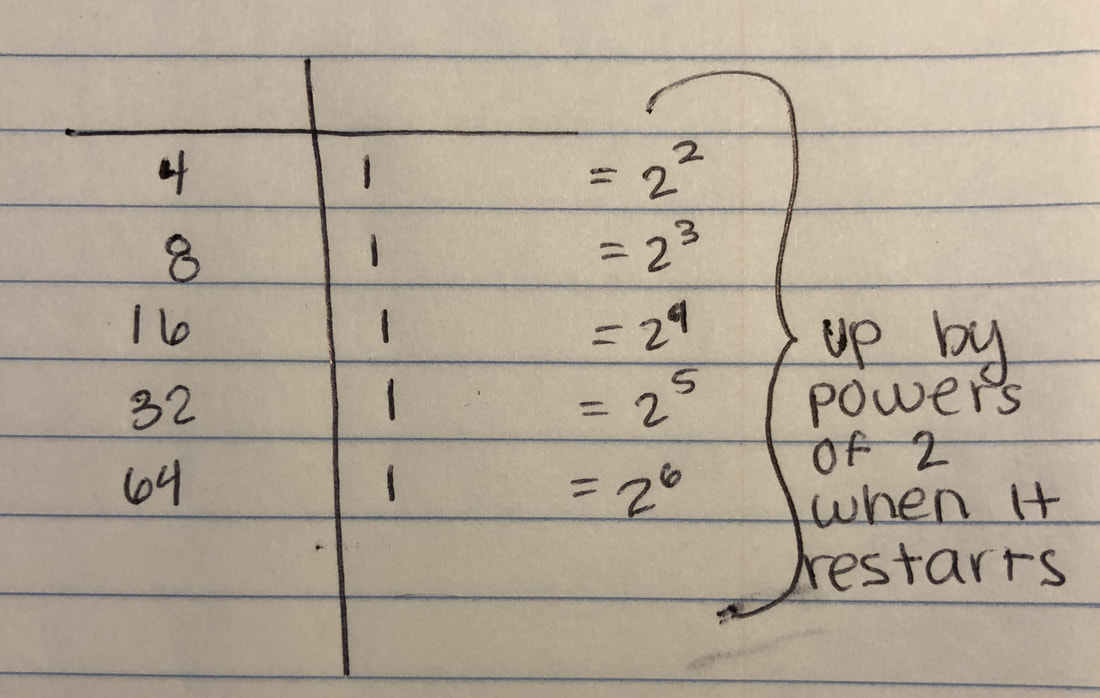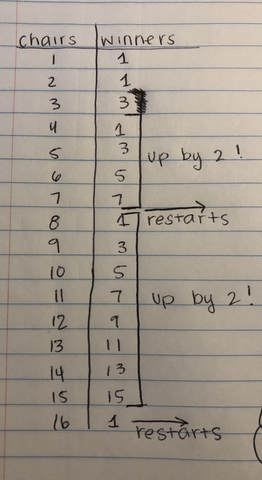Math TPOL
Growth Mindset Project!
The growth mindset project was basically for us to try to learn a new skill for two weeks, and at the end of the two weeks, we had to show a video that proved what we learned. For the growth mindset project, I decided to teach my dog how to do a few tricks. One week or a few days before the project was due, my dog got sick. This meant that I had to change it to something else. At first, I had picked this for a very simple reason, I love my dog.
The second thing I decided to learn was sign language. I decided to learn this for this project because of one of my classmates in my math class. She is always communicating by writing on a white board since no one else here knows sign language. At first, I wasn't sure of how to start, and what to do. I googled "sign language" and the first thing that popped up was a video! The video was of the ABC's in sign language. I started to practice this, and slowly started to get better at it. At first, it was very frustrating, but I was into it, so I felt motivated to keep going. In the end, I made a video of the first time I tried to spell out the ABC's in sign language, and until the first time I got it right. I am very proud of that video because I was able to show my growth.
This project really helped me understand my work ethic, and the best way for me to learn. In other words, it helped me get to know myself better. I now know that if I am very interested in a topic, I will try my hardest to do my best, no matter how many times I've failed. This helps me push myself because I really want to be successful in the topic I'm interested in.
After the two weeks was over, I downloaded an app on sign language. To be honest, I did use it for about three weeks, but I stopped. I started using it because I felt really proud of myself for learning the ABC's and how to count in sign language, so I wanted to push myself to learn more. In the end, I slowly started to lose interest in this. I honestly don't know why, but for now, I am glad I did this for my project.
I was able to apply this project to math by not giving up when I didn't understand something. I would ask questions until I was able to understand the topic, but I do admit that sometimes I didn't want to ask too many questions because I was scared and insecure. This project gave me the confidence I needed in the start of the junior year. It showed me that no matter how hard something is, if you keep trying for a certain amount of time, there will be a point where you'll get it. In math I was able to apply what I learned through this project.
Struggles with math problems!
This year, I struggled a lot with the Cow Problem. What we had to do with this problem was find how much area a cow could graze around a barn that is 10x10, and the cow was tied to a 100ft rope. I really struggled from beginning to end. When we were handed the worksheets, I didn't really understand how this was going to be solved. I understood what the problem was asking, but that was it.
Of course I asked my classmates for clarification and sometimes, it worked, but not most of the time. I would look at them confused, and soon give up on asking questions because I didn't want to seen dumb and to annoy them. I struggled with picturing how the rope kept getting shorter and shorter. At one point, the whole class was talking about a thing called the turning point. Up to this day, I still do not understand what was going on. I understand the math, but it is still very hard for me to understand and picture the problem from start to finish.
During the group quiz, I was very nervous because I knew I wasn't going to be able to contribute as much to help my group out. While working on it, I started to realize how I wasn't the only one confused in my group. This gave me the confidence to ask more questions about the problem. Doing so helped me understand the problem a bit more.
Struggles with content areas!
One content area that I really struggled was radicals. The definition of a radical is just a number with the radical sign in front of it. The definition sounds so easy, yet it is very hard for me to work with. Every since I started learning about this, I've never been good at it. It really stresses me out when they come up in a worksheet or a problem because it makes me feel slow. A lot of people are good at them and when I tell them I'm not, they give me a funny look. "What? It's something we learned in like fourth grade!" They say. These comments aren't meant to do harm, but they do. Every time it comes up in a work sheet, I get scared and skip it, hoping it'll go away.
I was really stressed because during the math final, a problem that was asking to leave the answer as radicals came up. As soon as I saw it, I skipped it. Again, hoping it would go away. When I was completely done with my test, #19 was the only one left. I sat there for about 15 minutes, trying to find a way of how to solve it. In the end, I ended up choosing that one as one of the ones I could skip.
Extras!
This year, I've grown a lot through my relationships/ friendships with people. The year I met a friend who would help me tremendously in math. With that person, I wouldn't feel ashamed to ask a lot of questions, and just be honest about what I struggled with. This friendship helped me grow because I realized that no matter how embarrassed I feel to ask a question, it is very important to do so. I obviously learned that through my first years at High Tech, but asking questions was something I still struggled with. Throughout this friendship, I started to feel more comfortable with myself. I was accepting that just because it takes me longer to understand a problem, it doesn't mean it's bad. This year, even though I struggled a lot in math, I can now say I am more comfortable with speaking up more.
Next year, I am planning on taking Pre-Calc. I was honestly considering taking Calculus, but I was scared to do so, and I still am. Taking Pre-Calc is my best choice. When the seniors came to our class to talk about what math class they chose and how it went, I decided I was not taking Calculus, for sure. Levi, one of the seniors that came in said something about how if your algebra isn't solid, it is probably not good idea to take calculus since most steps in a calculus problem are more algebra and one step of calculus. This really stood out to me, and helped me make the right decision.
Next year in math I plan on being successful as a senior by trying my best. The seniors that came to our class talked a lot about how studying is critical in order to be successful. Being completely honest, I have no idea how to study. It is something I have practiced for other classes, but not for math. It is one of my goals for next year to find what study habit works for me. This way, I know I'll be successful in math as a senior.
The growth mindset project was basically for us to try to learn a new skill for two weeks, and at the end of the two weeks, we had to show a video that proved what we learned. For the growth mindset project, I decided to teach my dog how to do a few tricks. One week or a few days before the project was due, my dog got sick. This meant that I had to change it to something else. At first, I had picked this for a very simple reason, I love my dog.
The second thing I decided to learn was sign language. I decided to learn this for this project because of one of my classmates in my math class. She is always communicating by writing on a white board since no one else here knows sign language. At first, I wasn't sure of how to start, and what to do. I googled "sign language" and the first thing that popped up was a video! The video was of the ABC's in sign language. I started to practice this, and slowly started to get better at it. At first, it was very frustrating, but I was into it, so I felt motivated to keep going. In the end, I made a video of the first time I tried to spell out the ABC's in sign language, and until the first time I got it right. I am very proud of that video because I was able to show my growth.
This project really helped me understand my work ethic, and the best way for me to learn. In other words, it helped me get to know myself better. I now know that if I am very interested in a topic, I will try my hardest to do my best, no matter how many times I've failed. This helps me push myself because I really want to be successful in the topic I'm interested in.
After the two weeks was over, I downloaded an app on sign language. To be honest, I did use it for about three weeks, but I stopped. I started using it because I felt really proud of myself for learning the ABC's and how to count in sign language, so I wanted to push myself to learn more. In the end, I slowly started to lose interest in this. I honestly don't know why, but for now, I am glad I did this for my project.
I was able to apply this project to math by not giving up when I didn't understand something. I would ask questions until I was able to understand the topic, but I do admit that sometimes I didn't want to ask too many questions because I was scared and insecure. This project gave me the confidence I needed in the start of the junior year. It showed me that no matter how hard something is, if you keep trying for a certain amount of time, there will be a point where you'll get it. In math I was able to apply what I learned through this project.
Struggles with math problems!
This year, I struggled a lot with the Cow Problem. What we had to do with this problem was find how much area a cow could graze around a barn that is 10x10, and the cow was tied to a 100ft rope. I really struggled from beginning to end. When we were handed the worksheets, I didn't really understand how this was going to be solved. I understood what the problem was asking, but that was it.
Of course I asked my classmates for clarification and sometimes, it worked, but not most of the time. I would look at them confused, and soon give up on asking questions because I didn't want to seen dumb and to annoy them. I struggled with picturing how the rope kept getting shorter and shorter. At one point, the whole class was talking about a thing called the turning point. Up to this day, I still do not understand what was going on. I understand the math, but it is still very hard for me to understand and picture the problem from start to finish.
During the group quiz, I was very nervous because I knew I wasn't going to be able to contribute as much to help my group out. While working on it, I started to realize how I wasn't the only one confused in my group. This gave me the confidence to ask more questions about the problem. Doing so helped me understand the problem a bit more.
Struggles with content areas!
One content area that I really struggled was radicals. The definition of a radical is just a number with the radical sign in front of it. The definition sounds so easy, yet it is very hard for me to work with. Every since I started learning about this, I've never been good at it. It really stresses me out when they come up in a worksheet or a problem because it makes me feel slow. A lot of people are good at them and when I tell them I'm not, they give me a funny look. "What? It's something we learned in like fourth grade!" They say. These comments aren't meant to do harm, but they do. Every time it comes up in a work sheet, I get scared and skip it, hoping it'll go away.
I was really stressed because during the math final, a problem that was asking to leave the answer as radicals came up. As soon as I saw it, I skipped it. Again, hoping it would go away. When I was completely done with my test, #19 was the only one left. I sat there for about 15 minutes, trying to find a way of how to solve it. In the end, I ended up choosing that one as one of the ones I could skip.
Extras!
This year, I've grown a lot through my relationships/ friendships with people. The year I met a friend who would help me tremendously in math. With that person, I wouldn't feel ashamed to ask a lot of questions, and just be honest about what I struggled with. This friendship helped me grow because I realized that no matter how embarrassed I feel to ask a question, it is very important to do so. I obviously learned that through my first years at High Tech, but asking questions was something I still struggled with. Throughout this friendship, I started to feel more comfortable with myself. I was accepting that just because it takes me longer to understand a problem, it doesn't mean it's bad. This year, even though I struggled a lot in math, I can now say I am more comfortable with speaking up more.
Next year, I am planning on taking Pre-Calc. I was honestly considering taking Calculus, but I was scared to do so, and I still am. Taking Pre-Calc is my best choice. When the seniors came to our class to talk about what math class they chose and how it went, I decided I was not taking Calculus, for sure. Levi, one of the seniors that came in said something about how if your algebra isn't solid, it is probably not good idea to take calculus since most steps in a calculus problem are more algebra and one step of calculus. This really stood out to me, and helped me make the right decision.
Next year in math I plan on being successful as a senior by trying my best. The seniors that came to our class talked a lot about how studying is critical in order to be successful. Being completely honest, I have no idea how to study. It is something I have practiced for other classes, but not for math. It is one of my goals for next year to find what study habit works for me. This way, I know I'll be successful in math as a senior.
Cow Problem
Problem Statement:
There is a barn that is 10x10. There is a cow attached to one corner of the barn with a 100ft rope. We had to find how much of the area the cow could graze.
Process:

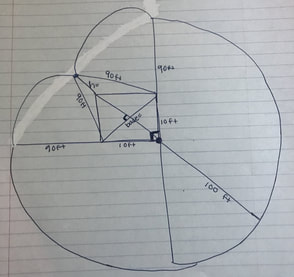
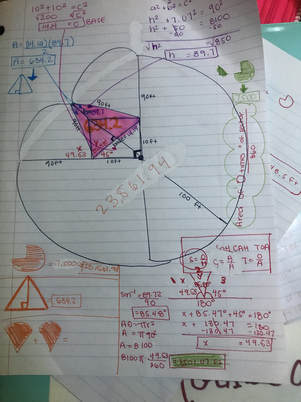
My first attempt to draw the diagram was just a square in the middle and a big circle surrounding it. At first, it seemed right, but then my group realized that the cow couldn't go around in a full circle because the rope was going to cut off. We knew it was going to be a weird circle, but we weren't really sure of how it was going to look. We decided to draw it out with the whole class, and this is what we got:
After finishing this diagram up, we knew something was off. What about the other part of the circle that was missing? We were stuck and didn't really know how to draw it out, until the class came together and drew it. It looked like this when it was done:
After finishing this diagram up, we knew something was off. What about the other part of the circle that was missing? We were stuck and didn't really know how to draw it out, until the class came together and drew it. It looked like this when it was done:
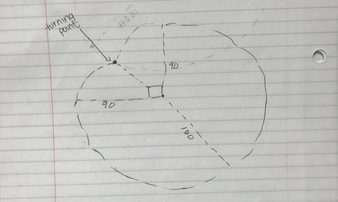
After drawing it, we knew we needed to cut this up into pieces that we knew how to solve the area for. We cut the circle in 3/4, then formed two triangles, and finally, what we call, the "pizza slices."
Solution:
We knew this was correct because the rope was getting shorter and shorter. We labeled it "turning point."
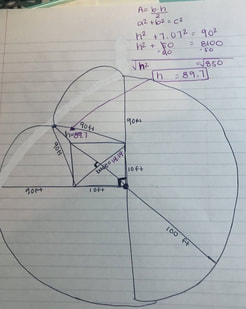
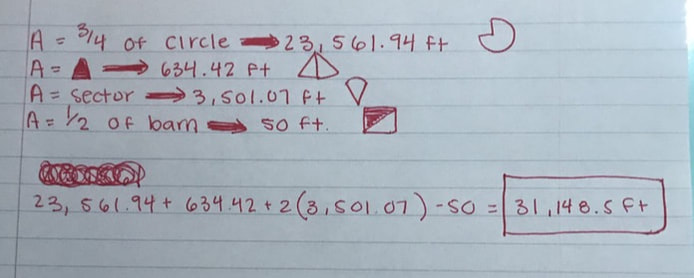
After this, we needed to break it down into pieces we needed to break it down into pieces we already knew how to solve for. For example, half a circle, or in this case, 3/4 of a circle. The formula for it was π r^2(.75)
Once we plugged it in and solved for it, the area for the 3/4 of the circle was 7,500. We had to do, 7,500*Pi = 23,561.9
After solving for this, we found more shapes that we knew how to solve for. For example, triangles. We cut out two triangles. At the end, our diagram looked like this:
Once we plugged it in and solved for it, the area for the 3/4 of the circle was 7,500. We had to do, 7,500*Pi = 23,561.9
After solving for this, we found more shapes that we knew how to solve for. For example, triangles. We cut out two triangles. At the end, our diagram looked like this:
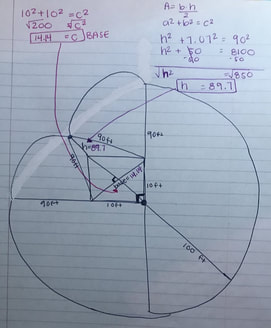
In order to find the area of those two triangles, we had to find the height first. We solved for it by using the pythagorean theorem.
Using this, we knew the height of the triangles was 89.7. Then we needed to find the base, so again we used the Pythagorean theorem. For the base, we got 14.14.
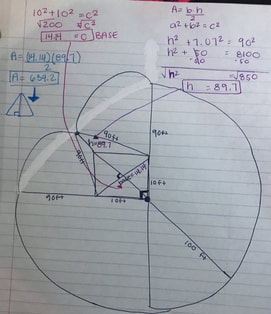
Finally, to find the area of the triangles, we were able to use A=b*h/2
This step was easy, we just had to plug the two answers in.
This step was easy, we just had to plug the two answers in.
For the area of the two triangles, we got 634.2 ft
Our next step, was to find the area of the pizza slices. To do this we had to use SOH CAH TOA. We needed to use this in order to find the angle measurements. We already knew that one of the angle measurements was going to be 45 degrees because one straight line is 180 degrees. We solved for the angle in the middle using SINE, inverse trig. In the red is how I solved for the angles. To find the third angle, we solved for x. We wanted to find a portion of the circle, so we but the angle measurement, (49.53) over 360. This gave us the answer to the pizza slices which was, 3,501.07.
Finally, to get the area of what the cow can graze, we added up all of our areas, and subtracted half of the barn which is 50ft. The answer was 31,148.5 ft.
Evaluation/ Reflection:
What pushed my thinking was my initial drawing and understanding of the cow problem. I didn't understand how the cow was going to go around the barn. I was just thinking about it going around the barn and it was all very confusing to me until we learned how to maximize the area that the cow was going to walk around. It also helped me a lot the final drawing with the "weird dimple thing" which was the turning point. I think that what I got the most out of this problem was slowing down, and again, not being scared to ask questions, even if the problem was already explained a thousand times, if I had questions, I know I needed to ask them. The group quiz affected me in a positive way. Once we were working on it, I realized how long the process was, and how much of the problem we were still missing. This helped me reach out to my friends after for help.
If I were to grade myself on this problem, I would give myself a solid B. I would give myself this because honestly, there were times when I wouldn't really try if I was confused because I was embarrassed. I would give myself this grade because even when I was confused I would still try to keep up and take as many notes to help me.
If I were to grade myself on this problem, I would give myself a solid B. I would give myself this because honestly, there were times when I wouldn't really try if I was confused because I was embarrassed. I would give myself this grade because even when I was confused I would still try to keep up and take as many notes to help me.
Maximum Rectangle
Problem Statement:
A rectangle has one corner on the graph of y=16-x^2 , another at the origin, a third on the positive y-axis, and the fourth on the positive x-axis. If the area of the rectangle is a function of x, what value of x yields the largest area of the rectangle?
Process:
|
|
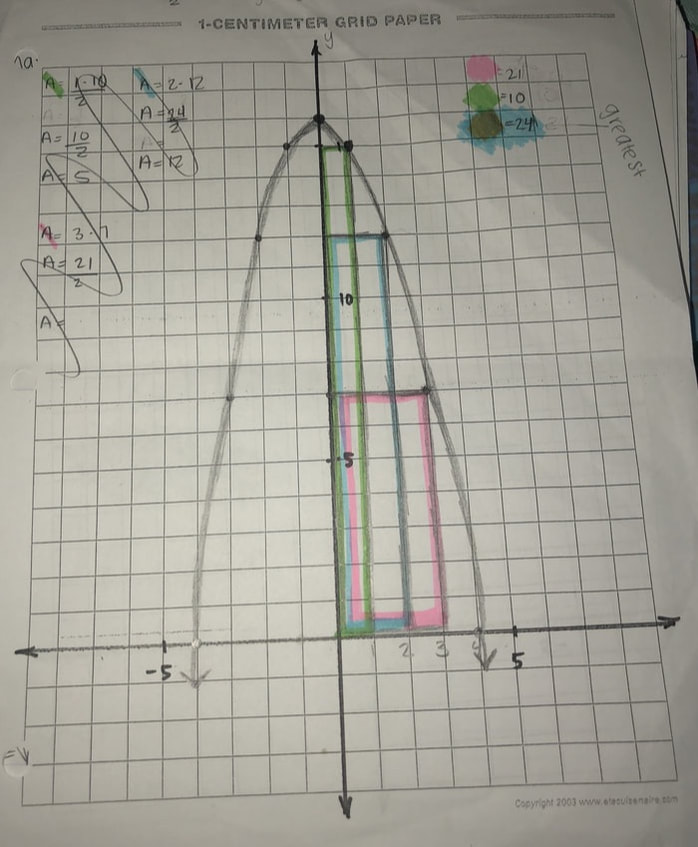
The first thing we did in order to fully understand the problem, we started by writing down a few questions. We shared them outloud and most of them were answered. After this, we plugged in numbers in our given equation which was y = 16 - x^2. We would plug in the the numbers in the x intercepts for x. This would give us points that would soon form into a parabola when we connected them. We knew that the y intercept was going to be 16. Inside the parabola we had to find a few rectangles, and find which one had the largest area. The rectangle with the largest area was the 2 by 12 which gave us an area of 24. This was our ESTIMATED area, not the final one. We noticed that we had to go by really small decimals, and we didn't want to keep going on forever, so we had to come up with an equation. The equation was A= 16x - x^3. It was now cubed because we needed to factor it out. Then, we needed to find an estimate for the perimeter, and again, like the last problem we needed to form an equation for it. We found the equation to be P=2x^2 +2x + 32. We know this because in order to find the perimeter, you need to add all the sides. Our first equation was P= 2( x+y), but then we plugged in our givens which were x and y. We knew that these equations were correct because once we graphed them, we were able to get both the maximum perimeter and maximum area.
|
Solution:
The solution for the maximum perimeter was 32.5 with the side lengths of (0.5, 15.75). We found this by using the equation we had, and turned it into vertex form. Once we found what the vertex was, we found out that the x was the width and the y was the maximum perimeter.
The solution for the maximum area was between 21 and 24. We used our equation to find it and we got 24.633609. Using this, our side lengths were 2.31 and 10.6639. The way we got this answer was by rounding to the hundredths place.
The solution for the maximum area was between 21 and 24. We used our equation to find it and we got 24.633609. Using this, our side lengths were 2.31 and 10.6639. The way we got this answer was by rounding to the hundredths place.
Group Test/ Individual Test:
Our group prepared for this group quiz by going over the Maximum Rectangle problem, then we worked on the practiced doing the practice quiz. The practice quiz was the same thing just with one different number. I honestly do not think we understood the whole problem very well. We were overthinking the whole thing a lot and we were making tables that were unnecessary. We struggled a lot with finding the actual area, we understood how to find the equations but not the final answer. My understanding for the individual quiz was very good, I was actually surprised. I think I was able to understand it because I didn't have my peers to make me overthink everything. The overall experience of the group quiz was good, but I think it distracted me a lot.
Evaluation/ Reflection:
What really pushed my thinking was how much my group struggled to fully understand this problem. I don't think I've ever been in a group where all of us are confused. This pushed my thinking because it made me put more effort in understanding the problem and trying to help my partners. I think that I got the most out of being able to solve this problem in multiple ways. For example, "plug and chug", making a table, graphing it, and actually solving the equation. I think I would give myself and A because I really did try my hardest to try to understand this problem even though I was confused most of the time.
Around King Arthur's Table Problem
Problem Statement:
Every time King Arthur had a prize, he would play a game with his knights and see who would be the winner. They would all sit around one table, and King Arthur would go around starting with knight in seat #1 and say "you're in", and with knight in seat #2 he would say "you're out." Then moving on, either "you're in" or "you're out" depending o what he had said before. The number of knights each day could vary. It could go from a small number such as 5 or up to 100 or more.
We were asked to create an equation that would help us find which seat would be the winner, no matter how many knights there were.
We were asked to create an equation that would help us find which seat would be the winner, no matter how many knights there were.
Process:
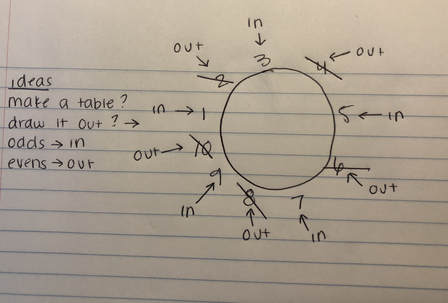
Our first step was to make a drawing. As a group, we drew a big circle that represented the table, we started off with 10 knights to make it easier. We did notice that odds were in and evens were out. This was one pattern that we saw. But we needed to know more in order to create a formula that would give us the winner. We noticed that this was very confusing, so we started doing a table. It was more straightforward and easier to see the pattern. We noticed that it would restart back at 1 whenever the knight in a chair was a multiple of two. For example, 4, 8, 16, 32, and 64.
Solution:
At the end, we found out an equation that would get us the winner, no matter how many knights there were. My group didn't find this equation, another group did. We were asked to explain why it worked. My group didn't really know how to explain it since we were barely getting the hang of the pattern, so we wrote out what we knew.

The equation was y=(k x 2^x) 2+1. We would plug in which chair/knight we were trying to find the winner for. Then, we would plug in a power for each number that was closer. This was very difficult because it was kind of hard to figure out up to which number to raise the 2 to, at least for me it was.
At the end, Mr. Carter had told us that we could use logarithms to make it easier, but my group and I forgot how to do it, so we just left it at that since it worked.
At the end, Mr. Carter had told us that we could use logarithms to make it easier, but my group and I forgot how to do it, so we just left it at that since it worked.
Evaluation/ Reflection:
I am honestly very proud of myself. I feel like I was able to help my group a lot by contributing new ideas and asking questions. Most of the time they weren't questions about what we could do, but when I was confused about a step or a pattern that we noticed. This really helped because every time I asked something, someone in our group would realize something new or find a mistake.
I would give myself an A because I did try very hard to understand this problem. I'm very happy because I actually really enjoyed and found this problem very interesting.
I would give myself an A because I did try very hard to understand this problem. I'm very happy because I actually really enjoyed and found this problem very interesting.